Learning an Optimized Simulation
Oct 14, 2022 | Jagannath Rajagopal | 5 min read
Let’s discuss a common pattern where you combine simulation, optimization and learning.
This can be applied in situations where the solution space and the problem space are not the same.
Take “design” as an example: design configurations are obtained from the solution space, and the design objective (the criteria the design needs to meet — or — the goal its attempting to accomplish) lives in the problem space. The problem space generally is characterized by more dimensions and is sometimes thought of as the combination of the solution space and an environment space.

Training an optimization or a learning model involves iteratively adjusting your solution for each iteration to meet an objective.
Both of these tasks are not straightforward if part of the problem space lies outside the solution space — one, the model won’t know how a particular set of solutions performed and two, as a result, it won’t know how to traverse the solution space aka where to look for a better solution.
If you have data on solution configurations, environment parameters, and performance of each solution, you can pre-train a model between solution and problem objectives — based upon certain environmental conditions.
You could then use this model to estimate the design objective for every solution configuration the solving process encounters.
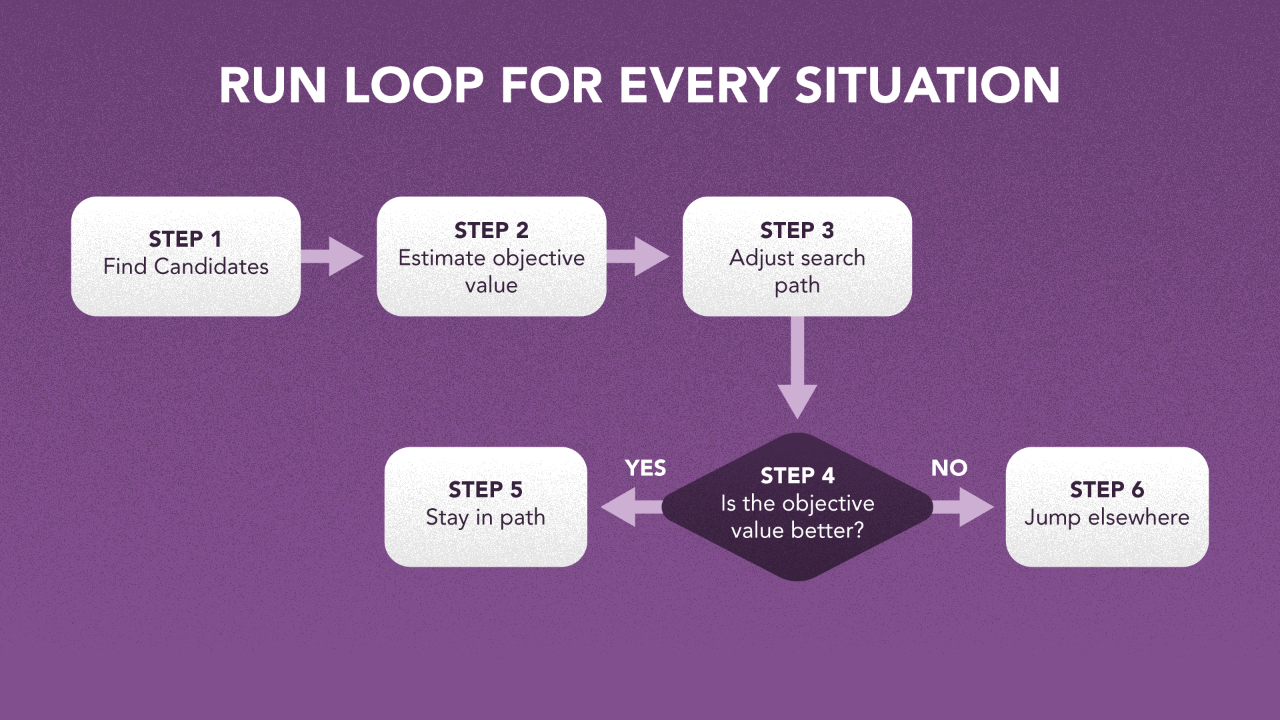
If you are looking to maximize this objective, you are left with a two-step process, each run in a loop for every iteration:
Step 1 — Find a set of candidate solutions
Step 2 — Estimate objective value for each candidate (using the pre-trained learner), and adjust search path/neighborhood based on this. If the objective value is getting bigger, stay and search in the neighborhood. If not, jump to a different part of the solution space.
I’ve created a LOT of resources on this topic. Here’s my course on Design Thinking for Hero Methods. Here’s my YouTube channel with previews of course videos. Here’s my website; navigate through the courses to find free previews & pdfs.
- - -
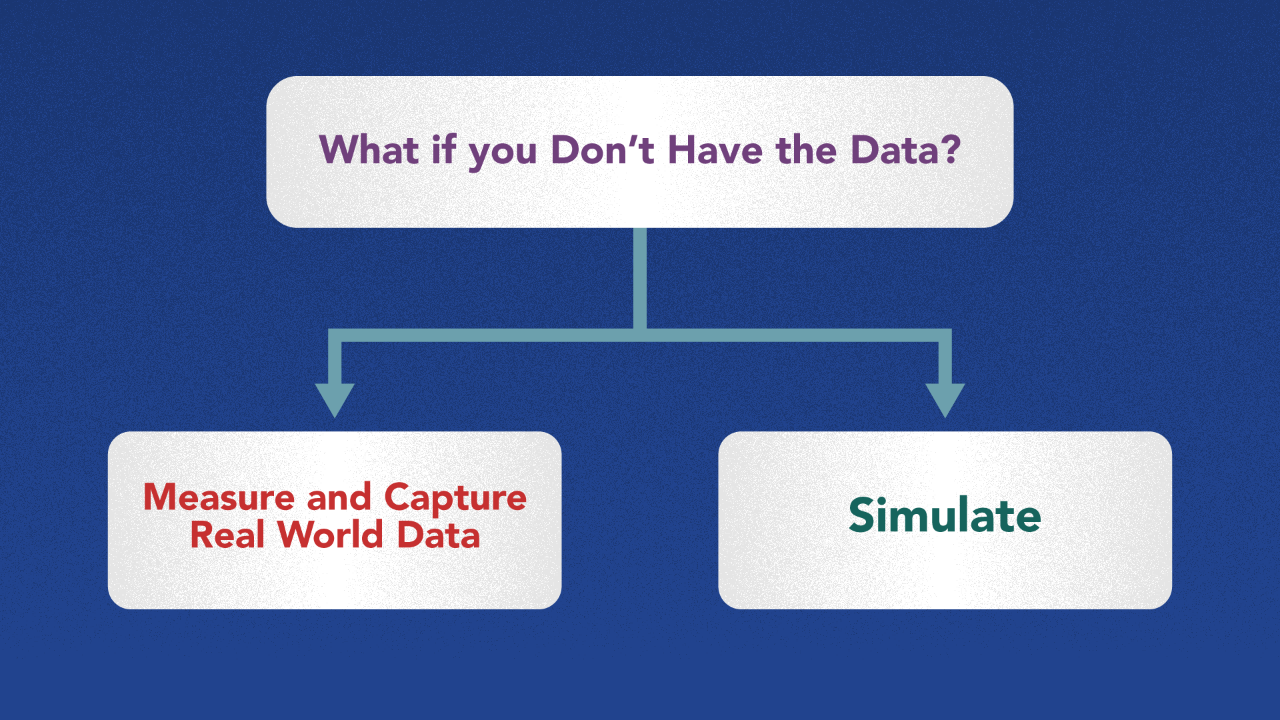
So what happens if you don’t have the data?
One way is to measure and capture the data in the real-world — however — this may not be feasible for many problems. There may be too many solutions with each one taking too long or too much to measure.
Another approach is to simulate the performance of your solutions for different environments, and capture data this way.
Note that every time you change your solution, the data you capture will be different. Use this data to teach a surrogate model that estimates your objective for different potential solutions or environments.
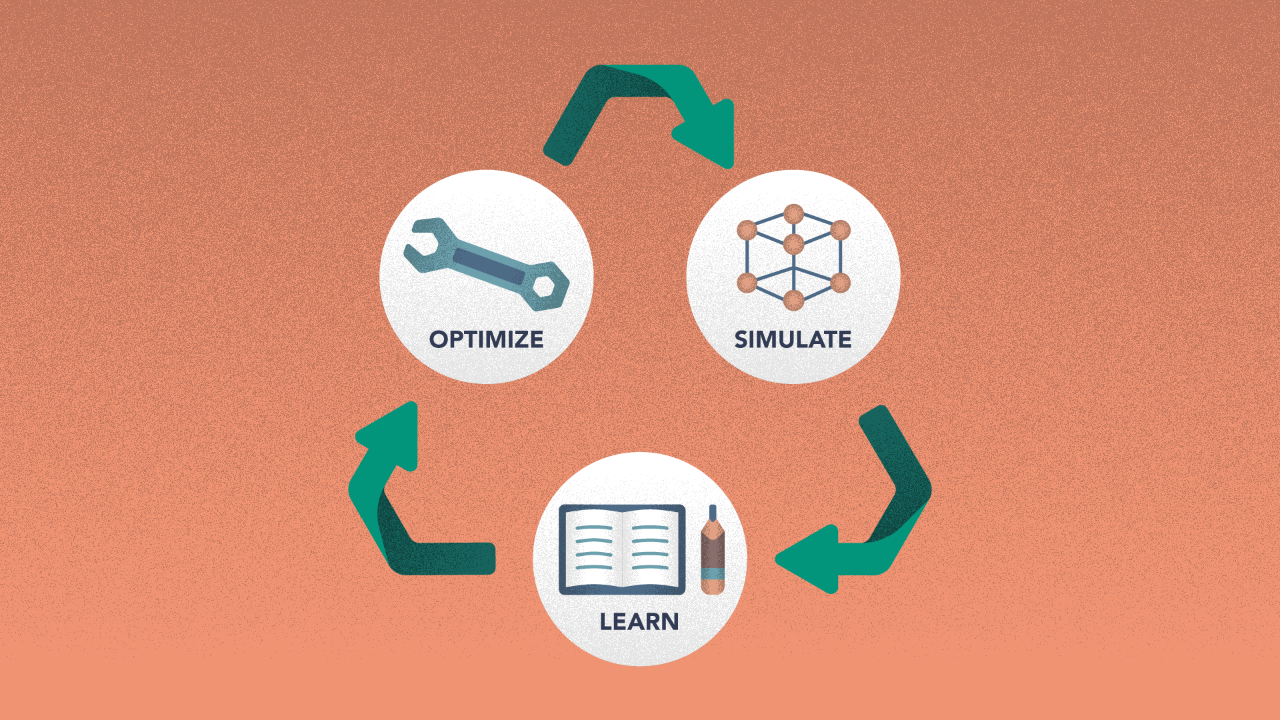
This approach involves 3 steps that are run in a loop for every iteration.
Step 1 — Optimize — Picking the best — or many of the top — solution(s).
Step 2 — Simulate — Use the solutions from step 1 to simulate system performance for different environmental factors.
Step 3 — Learn — Once you have enough data, teach a learning surrogate model that replaces the simulation, or alternately advises on the best simulations to run. Use that model to determine search direction and iterate back to Step 1.
The 3 steps are used in a cycle to continually narrow down and improve the quality of a complex solution in a multi-dimensional problem space.
This is regularly used in Generative Design in cases where surrogate learners are tasked with reducing computational cost in engineering design.
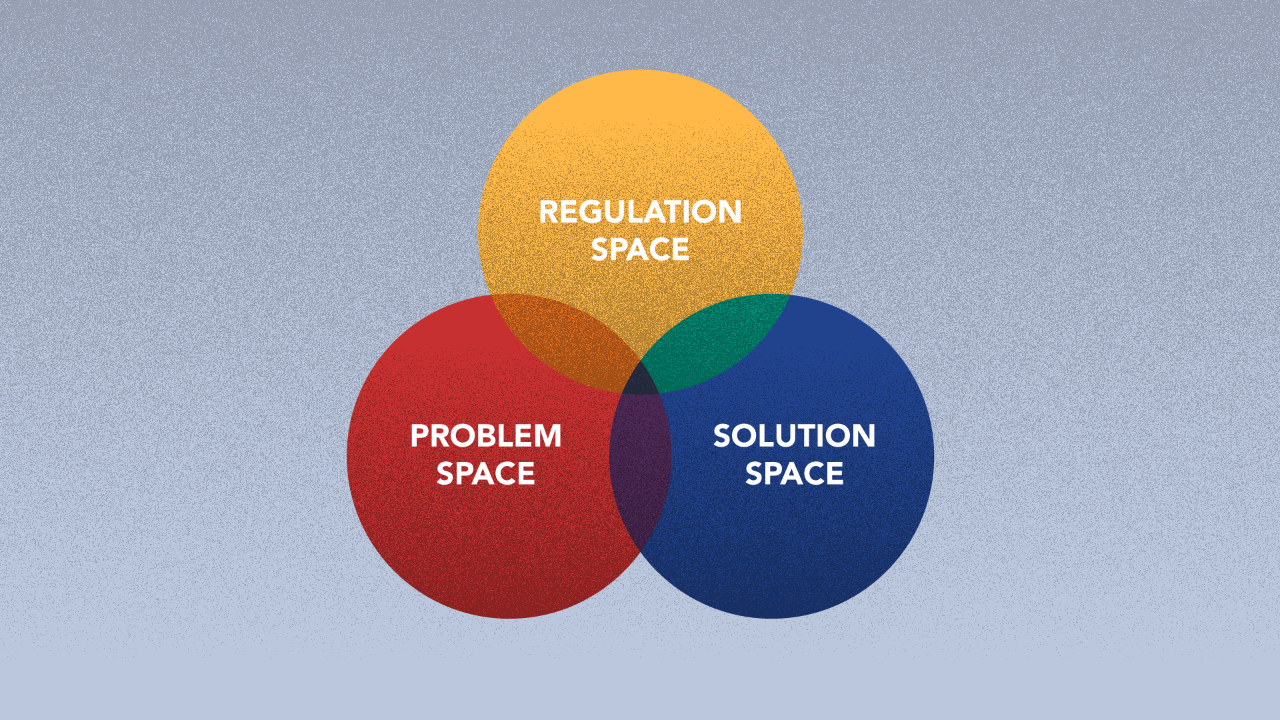
Here is a thought experiment — what if you need to introduce complex multi-dimensional constraints?
If so, now you are left with a problem space, a solution space and a constraint space.
If the solution needs to meet regulatory requirements, the constraint space may be thought of as a combination of the solution space and the regulation space, and may be different from the problem space. How does the process of solving change then? Use the above thinking to expand it.
The approach of combining learners, optimizers and simulators may also be used in parameter selection while training complex Hero Models.
Mathematical processes that solve complex problems — such as evolutionary algorithms — oftentimes include parameters that influence how they work. All other things being equal, changing these parameter values results in different solutions to your problem.
At that point, performance metrics may be used to figure out which of those solutions are right for the problem, and by extension which parameter sets.
In some problem spaces, like neural network learning, the relationship between the parameter set and performance metrics may in themselves be treated as a complex data-driven problem — data-driven because you’ll have data on parameter set vs performance metric. You can choose to simulate, optimize, or learn this to see how well the neural network is encoded.

At Kado, we like to surface patterns like this. If there are use cases of two or more methods — from different families — working together, that really excites us. We have a few more like this in our library. If you have ideas or know of approaches like this, we are happy to listen.
This is how we see the world
Machine Learning is King, but of narrow territory. Hero Methods do things that ML cannot. Taken together, not only do they help solve complex problems, they also lay the doorway to AI.
Get in touch
-
Milton, ON L9T 6T2, Canada
-
help@kado.ai
-
+1 416 619 0517
Copyright © 2026
Super!
An email is on it's way.
Super!
An email is on it's way.

